Сезон 2009-2010
Новые правила
В игре могут принимать участие учащиеся 7-10 классов
----- В каждом туре
участникам конкурса предлагаются по 10 задач
определенной темы, решение которых следует сдать в указанные сроки
своему учителю математики или в кабинет 303.
----- «Стоимость» каждой
задачи – 120 баллов, которые делятся поровну
между всеми, правильно решившими
данную задачу.
----- По каждой теме предлагается
презентация возможного способа решения, но допускается решение любым способом.
----- Даты поступления
решений на проверку и результаты проверки
отражаются в электронном протоколе.
----- Решение каждой задачи
надо записать на отдельном листе (можно использовать бланки для записи решения,
которые удобно печатать 2
страницы на листе в меню ПЕЧАТЬ, ОКОНЧАТЕЛЬНАЯ ОБРАБОТКА).
На
листке с решением не забудьте указать:
o
Фамилию Имя
o
Класс
o
№ задачи
o
Дата сдачи
решения
(*) Если, сдав решение, Вы
обнаружили ошибку, то можно сдать новое
решение в указанные сроки. В этом случае первое решение не проверяется. В случае неоднократного решения одной и той же задачи проверке подлежит
только последний вариант.
----- Проверка решения будет
осуществляться организаторами конкурса в течение 2-х недель со дня завершения приема решений. После
проверки планируется разбор задач (для желающих). Решения задач публиковаться
на сайте не будут
----- Итоги каждого тура
проводятся независимо друг от друга
6
тур. КЕНГУРУ 2000,
7-8 класс
Сроки проведения: 1
марта - 31марта
бланки для записи решения, протокол
Конкурс
«Кенгуру» возник в Австралии по инициативе известного австралийского математика
и педагога Питера Холлорана и быстро
распространился по странам и
континентам. В 1994 году Россия впервые приняла участие в этом конкурсе.
18 марта 2010 года состоится очередная
игра «КЕНГУРУ 2010», а в шестом
раунде школьного конкурса предложены
задачи, которые участники «Кенгуру» решали 10 лет назад.
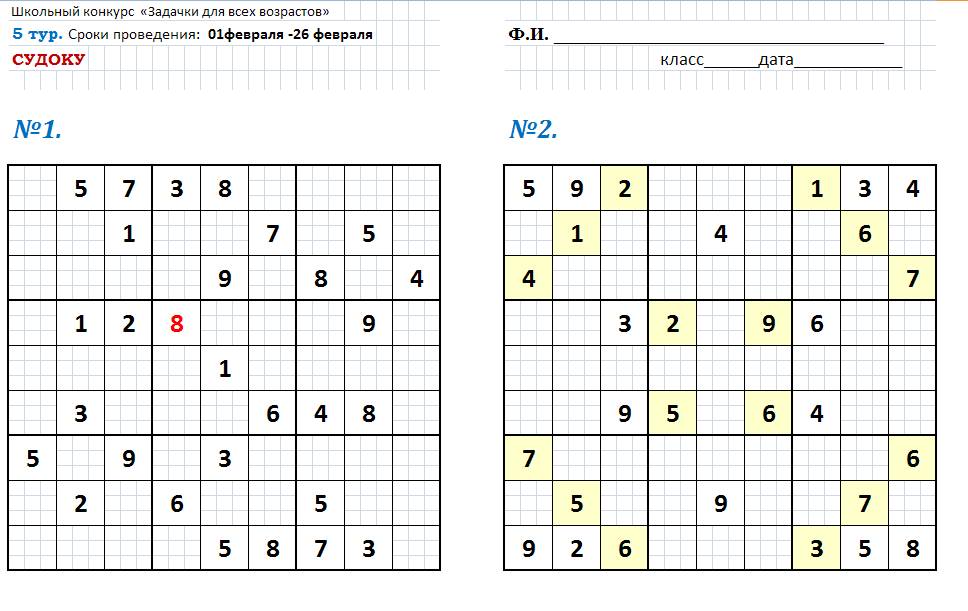
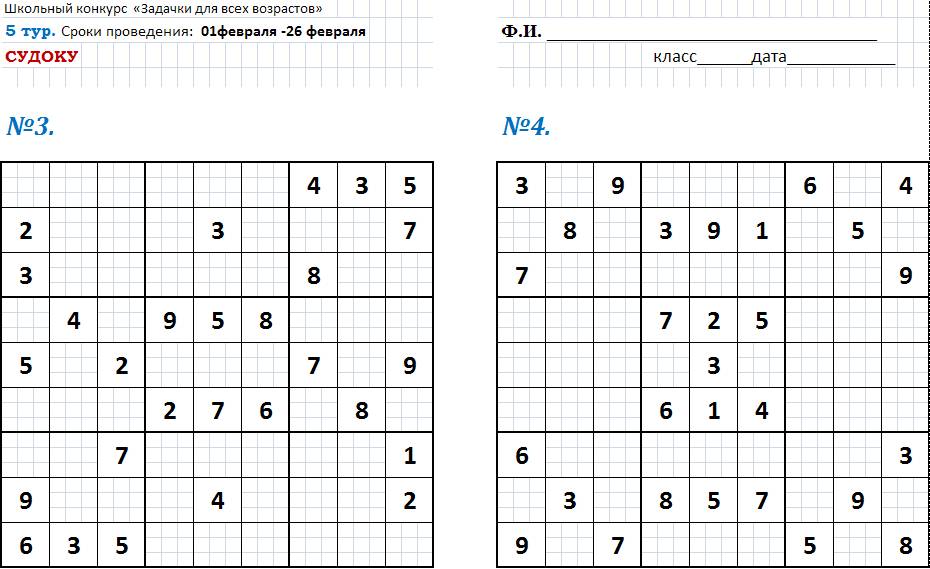
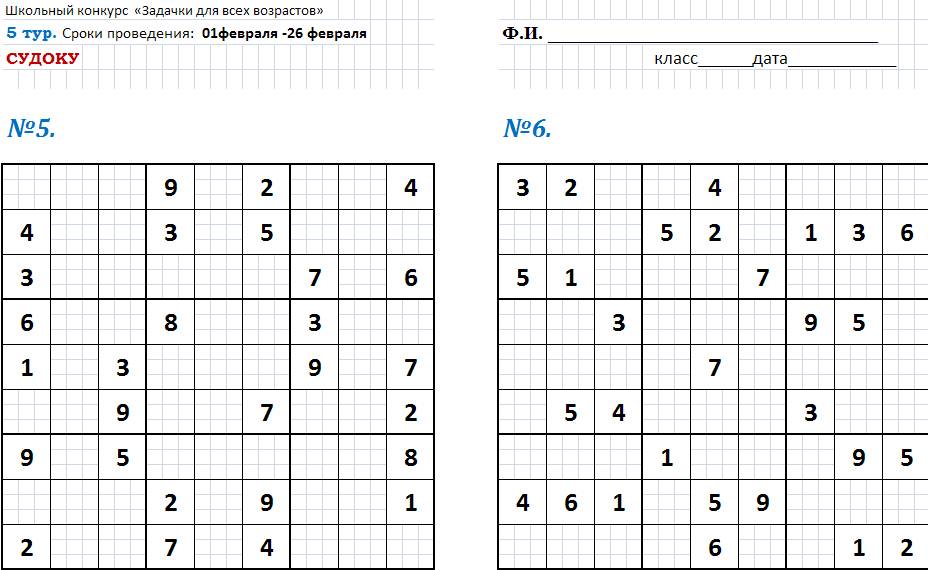
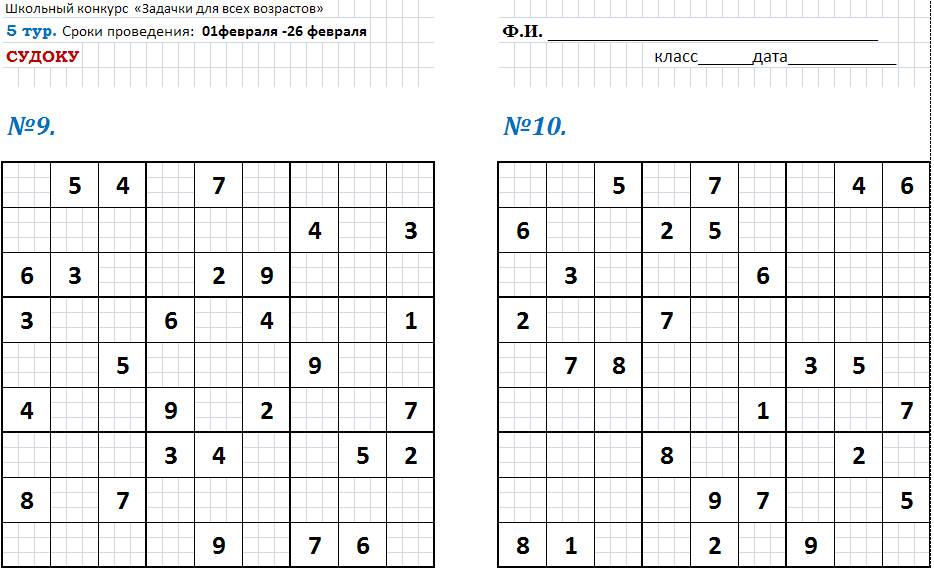
5
тур. Судоку
Сроки проведения: 1
февраля - 26 февраля
Презентация, образец
решения, форматка образца
бланки для записи решения (см.
образец, вторая страница), протокол,
наградной
лист
|
|
|
|
|
|
|
|
|
|
4
тур. Круги Эйлера
Сроки проведения: 11
января - 29 января
Презентация, немного
истории, основные понятия,
условия задач, бланки
для записи решения, протокол, наградной
лист
по материалам исследовательской работы Захаренко Андрея, ученика 7 класса
«Сторожевской
средней общеобразовательной школы» с. Сторожевск Корткеросского района,
опубликованной в Издательском Доме «Первое сентября» в
разделе «Портфолио»
|
|
1.
|
В классе
учатся 40 человек. Из них по русскому языку имеют «тройки» 19 человек, по
математике – 17 человек и по истории – 22 человека. Только по одному предмету
имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека, по истории – 11
человек. Семь учеников имеют «тройки» и по
математике и по истории, а 5 учеников – «тройки» по всем предметам.
Сколько человек учится без «троек»? Сколько человек имеют «тройки» по двум из
трех предметов? |
|
|
2.
|
В классе 35 учеников, из них 20
занимаются в математическом кружке, 11 - в биологическом, 10 ребят не
посещают эти кружки. Сколько биологов увлекается математикой? |
|
|
3.
|
На полу
площадью 12м2 лежат три ковра: площадь одного 5м2,
другого - 4м2 и третьего - 3м2. Каждые два ковра
перекрываются на площади 1,5м2, причем
0,5м2 из этих полутора квадратных метров приходится на участок
пола, где перекрываются все три ковра. а) Какова
площадь пола, не покрытая коврами? б) Какова
площадь пола, покрытая одним только первым ковром? |
|
|
4.
|
Староста одной группы института попал в деканат
следующие сведения о студентах: «В группе учатся 45
студентов, из которых 25 юношей. 30 студентов учатся на оценки «хорошо» и
«отлично», в том числе 16 юношей. 28 студентов занимаются спортом, в том числе 18 юношей и 17 студентов,
учащихся на оценки «хорошо» и
«отлично». 15 юношей учатся на «хорошо» и «отлично» и при этом занимаются спортом». В представленных данных была найдена
ошибка. В чем она состоит? |
|
|
5.
|
В офисе
туристической фирмы работают сотридники, каждый из которых знает хотя бы один
иностранный язык. 6 человек знают английский, 6 – немецкий, 7-
французский, 4 знают английский и немецкий, 3 – немецкий и
французский, 2 – французский и английский. Все три языка знает один
сотрудник. Сколько человек работают в офисе туристической фирмы? Сколько
человек из них знают только английский язык? |
|
|
6.
|
Когда-то
давно в нашей стране были пионеры и комсомольцы, и они носили соответственно пионерские
галстуки и комсомольские значки. В одной экскурсии участвовали семиклассники
и восьмиклассники. Все они были либо с комсомольскими значками, либо в
пионерских галстуках. Мальчиков было 16, комсомольцев и комсомолок всего 24.
Пионерок столько, сколько мальчиков-комсомольцев. Сколько всего ребят
участвовало в экскурсии? |
|
|
7.
|
В 5 классе
нашей школы 22, в 6 классе – 16, в 7 классе – 23 ученика. Известно, что в
секции по лыжам, шахматам и спортивным
играм ходят 4 человека. Каждые 2
секции посещают 9 человек. Сколько
человек из каждого класса ходит
на секции? Сколько учеников каждого класса
не ходит ни в какую спортивную
секцию? |
|
|
8. |
В классе 32
человека. Из них 14 играют в баскетбол, 24 - в пионербол, 16 - в волейбол. Увлекаются
двумя видами спорта - баскетболом и пионерболом - шестеро, баскетболом и
волейбол - четверо, пионерболом и волейболом - четверо. Двое ни чем не
занимаются. Сколько ребят увлекается всеми видами игр? |
|
|
9. |
Ребятам поручили
изготовить кубики. Несколько кубиков сделали из картона, а остальные из
дерева. Кубики были двух размеров: большие и маленькие. Часть из них
покрасили в зеленый цвет, другую – в красный.
Получилось 16 зеленых кубиков. Зеленых кубиков большого размера было 6. Больших зеленых из картона было 4.
Красных кубиков из картона было 8,красных кубиков из дерева – 9. Больших
деревянных кубиков было 7, а маленьких деревянных кубиков было 11. Сколько же
всего получилось кубиков? |
|
|
10.
|
Ребят, которые
хотят обмениваться различного рода журналами, собралось 10 человек. Среди них выписывают «Квант» -
6 человек, «Техника молодежи» –
5 человек, «Юный натуралист» – 5 человек, «Квант» и «Техника молодежи» – 3
человека, «Техника молодежи» и «Юный натуралист» -2 человека, «Квант» и «Юный натуралист» – 3 человека, а один человек не выписывает
ни одного журнала, но читает все эти журналы в библиотеке. Надо узнать, сколько человек выписывают все
три журнала, сколько – два, а сколько – только один журнал. |
3
тур. Задачи на
переливания (бильярдный способ решения)
Сроки проведения: 2
ноября-29 ноября
Презентация, условия
задач, бланки для записи решения, протокол, наградной
лист
|
|
1.
|
Две
группы альпинистов готовятся к восхождению. Для приготовления еды они используют
примусы, которые заправляют бензином. В альплагере имеется 10-литровая
канистра бензина. Имеются еще пустые сосуды в 7 и 2 литров. Как разлить
бензин в два сосуда по 5 литров в каждом? |
|
|
2.
|
Как разделить поровну между двумя семьями 12 литров
хлебного кваса, находящегося в двенадцатилитровом сосуде, воспользовавшись
для этого двумя пустыми сосудами: 8-литровым и 3-литровым? |
|
|
3.
|
Летом
Винни Пух сделал запас меда на зиму и решил разделить
его пополам, чтобы съесть половину до Нового Года, а другую половину - после
Нового года. Весь мед находится в ведре, которое вмещает 6 литров, у него
есть 2 пустые банки - 5-литровая и 1-литровая. Может ли он разделить мед так,
как задумал? |
|
|
4.
|
Белоснежка
ждет в гости гномов. Зима выдалась морозной и снежной, и Белоснежка не знает
наверняка, сколько гномов решатся отправиться в
далекое путешествие в гости, однако знает, что их будет не более 12. В ее хозяйстве
есть кастрюлька на 12 чашек, она наполнена водой, и две пустых - на 9 чашек и
на 5. Можно ли приготовить кофе для любого количества гостей, если угощать
каждого одной чашкой напитка? |
|
|
5.
|
Нефтяники
пробурили скважину нефти. Необходимо доставить в лабораторию на экспертизу 6
литров нефти. В распоряжении имеется 9-литровый и 4-литровый сосуды. Как с
помощью этих сосудов набрать 6 литров? |
|
|
6.
|
Бидон ёмкостью 10 л
наполнен молоком. Требуется перелить из этого бидона 5 л в семилитровый
бидон, используя при этом ещё один бидон, вмещающий 3 л. Как это сделать? |
|
|
7.
|
Можно ли отмерить 8 л
воды, находясь у реки и имея два ведра: одно вместимостью 15 л, другое
вместимостью 16 л? |
|
|
8.
|
Есть три бидона емкостью 14, 9 и 5 литров. В большом
бидоне 14 л молока, остальные пусты. Как с помощью этих бидонов разделить
молоко пополам? |
|
|
9.
|
Имея два полных
десятилитровых бидона молока и пустые четырехлитровую и пятилитровую
кастрюли, отмерьте по два литра молока в каждую кастрюлю. |
|
|
10. |
Имеется три сосуда без
делений объемами 6 л, 7 л, 8 л, кран с водой, раковина и 6л сиропа в самом
маленьком сосуде. Можно ли с помощью переливаний получить 12 л смеси воды с
сиропом, так чтобы в каждом сосуде воды и сиропа было поровну? |
Решение может быть представлено в виде
таблицы переливаний
2
тур. Логические
задачи (табличный способ решения)
Сроки проведения: 5
октября-25 октября
Презентация 1, презентация 2,
условия задач, бланки
для записи решения, протокол, наградной
лист
|
1.
|
Куда налит квас? |
|
2.
|
Три подруги Три подруги вышли погулять в белом, зеленом и синем платьях и туфлях
таких же цветов. Известно, что только у Лили цвет платья и цвет туфель совпадают.
Ни туфли, ни платье Вали не были белыми. Наташа была в зеленых туфлях.
Определите цвет платья и туфель на каждой из подруг. |
|
3.
|
Три брата Три брата Иван, Дмитрий и Сергей — преподают
различные дисциплины в университетах Москвы, Петербурга и Казани. Иван
работает не в Москве, а Дмитрий не в Петербурге. Москвич преподает не
историю. Тот, кто работает в Петербурге, преподает химию. Дмитрий преподает
не биологию. Какую дисциплину преподает Сергей в университете, какого города? |
|
4.
|
Кто где живет? |
|
5.
|
Кого как зовут? |
|
6.
|
Четыре
девушки |
|
7.
|
Отпуск В течение последних четырех лет инженеры Еремин, Фомин, Демин и Вовин
получают очередные отпуска в мае, июне, июле и августе. Причем если один из
них отдыхает в мае, то другой в июне, третий в июле, а четвертый в августе.
Так, в первый год Демин отдыхал в июле; во второй год Демин отдыхал в
августе, а Еремин в мае. На третий год Вовин отдыхал в июне, а Фомин на
четвертый год в июле. Требуется узнать время отдыха каждого инженера в
течение четырех лет. |
|
8.
|
Пять друзей В небольшом городке жили пять друзей Иванов, Петров, Серов, Зуев и
Асеев. Профессии у них: маляр, мельник, плотник, актер, парикмахер. Петров и Зуев
никогда не держали в руках малярной кисти. Иванов и Зуев собираются посетить
мельницу, на которой работает их товарищ. Петров и Иванов живут в одном доме
с актером. Иванов и Серов каждое воскресенье играют в городки с плотником и
маляром. Петров брал билеты на футбол для себя и для мельника. Кто кем был? |
|
9.
|
Кто есть кто? |
|
10.
|
Три студента Три студента Андреев, Борисов и Воронов учатся на различных
факультетах педагогического института (историческом, математическом и
иностранных языков). Все они приехали из различных городов: Талина, Твери,
Тамбова. Причем один из них увлекается футболом, другой баскетболом, третий
волейболом. |
1
тур. Задачи о
турнирах (решение с помощью графов)
Сроки проведения: 7
сентября-27 сентября
Презентация, условия
задач, бланки
для записи решения, протокол , ответы и
комментарии к решениям
|
1.
|
В шахматном турнире
по круговой системе участвуют 8 школьников. Известно, что Миша и Петя сыграли
по 7 партий, Саша – 5, Костя и Женя – по 4, Гриша и Ваня – по 2. С кем сыграл
восьмой участник, Вова, если Костя и Женя сыграли между собой? |
|
2.
|
В шахматном
турнире по круговой системе участвуют 5 школьников. Известно, что Миша и
Саша провели по 4 встречи, Костя и
Женя – по 3, Ваня – 2. С кем сыграл Ваня? |
|
3.
|
В шахматном
турнире по круговой системе участвуют 8 школьников. Известно, что Миша и
Леша, Илья и Женя сыграли между собой. Кроме этого известно, что Ваня провел
7 встреч, Саша – 5, Илья, Женя, Аркадий и Петя – по 3, Миша и Леша – по две.
Кто с кем сыграл? |
|
4.
|
В шахматном
турнире по круговой системе участвуют 6 школьников. Известно, что Кеша сыграл
5 партий, Толя – 4, Семен – 2, Вася -1. Сколько встреч провели еще 2
участника: Андрей и Саша? |
|
5.
|
В шахматном
турнире по круговой системе, в котором участвуют 6 школьников, сыграно 10
партий. Известно, что каждый участник сыграл не менее двух встреч, Ваня
провел 4 встречи, а Миша – 3. Сыграл ли еще кто-нибудь, кроме Вани, больше,
чем Миша, если Ваня и Миша между собой не встречались? |
|
6.
|
В футбольном
турнире по круговой системе, в котором участвуют 4 команды 5-х классов и 3 команды
4-х классов, проведено 13 матчей. Известно, что команды 5 «А» и 5 «Б» классов
провели все свои встречи. Какое наименьшее число встреч провела команда? |
|
7.
|
В шахматном
турнире по круговой системе, в котором участвуют 4 школьника и все сыграли
хотя бы по одной встрече, только Ваня и Леша провели одинаковое число встреч.
Сколько встреч провели Ваня и Леша? |
|
8.
|
В шахматном
турнире по круговой системе, в котором участвуют 5 школьников и все сыграли хотя бы по одной встрече,
только Ваня и Леша провели одинаковое число встреч. Сколько встреч провели
Ваня и Леша? |
|
9.
|
Марсиане очень
любят танцевать танцы, в которых нужно браться за руки. В танце «Пирамидка»
может участвовать не более 7 марсиан, у каждого из которых не более трех рук.
Какое наибольшее число рук может быть у всех танцующих вместе, если любая
рука одного марсианина держит ровно одну руку другого марсианина? |
|
10.
|
В танце «Большая
пирамида» может участвовать не менее 7 марсиан, у каждого из которых не менее
пяти рук. Какое наименьшее число рук может быть у
танцующих, если любая рука одного
марсианина держит ровно одну руку другого марсианина? |
7
тур. …….
Сроки проведения: …
апреля -… апреля
Презентация,
условия задач, бланки
для записи решения, протокол
8
тур. …….
Сроки проведения: … мая
-… мая
Презентация,
условия задач, бланки
для записи решения, протокол
Архив конкурса


|
Правила участия Ежедневно (пять раз в неделю) участникам предлагается по одной
задачке, для решения
которых достаточно знаний
стандартных арифметических действий и умения логически рассуждать. Цель игроков –в течение дня решить предложенную
задачу и устно рассказать это решение учителю или «главному решателю данной задачи» своего класса. «Главным решателем
данной задачи» становится участник конкурса, первым
предложивший правильное решение. Каждое правильное решение оценивается бонусным баллом: «Главный решатель данной задачи» - 5 балов (в течение
дня он ведет статистику решаемости задачи); Второй и третий «решатели» - по 3
балла; Четвертый и пятый «решатели» - по 2
балла; Все остальные «решатели» - по 1
баллу. Каждые 20 бонусных баллов могут быть переведены в
дополнительную отметку «5» по математике. По желанию участника
пересчет может вестись по курсу 16 баллов – «4» |

08 декабря – 13 декабря 2008 №№1-5
15 декабря – 20 декабря 2008
№№6-10
22 декабря – 27 декабря 2008
№№11-15