Самостоятельная работа 3 по теме "Независимые события"
1. События
U и V независимы. Найдите вероятность наступления события U ![]() V, если
P(U) = 0, 3, P(V) = 0, 5.
V, если
P(U) = 0, 3, P(V) = 0, 5.
Решение.
(+) События называются независимыми, если
P(U ![]() V ) = P(U ) ∙ P( V )
V ) = P(U ) ∙ P( V )
Значит, P(U ![]() V ) = 0,3 ∙
0,5 = 0,15
V ) = 0,3 ∙
0,5 = 0,15
2. События
K и L независимы. Найдите вероятность события K, если P(L) = 0, 9, P(K ![]() L)
= 0, 72.
L)
= 0, 72.
Решение.
(+) Для независимых событий выполняется равенство
P(К ![]() L ) = P(K )
∙ P( L )
L ) = P(K )
∙ P( L )
0,72 = P(K ) ∙ 0,9
P(K ) = 0,72 : 0,9 = 0,8
3. Монету бросают два раза. Выпишите все элементарные события этого эксперимента. Событие A — первый раз выпал орел. Событие B — второй раз выпала решка. Найдите вероятность каждого из этих событий и вероятность их пересечения. Являются ли эти события независимыми?
Решение.
(+) Вероятностное поле ОО; ОР; РО; РР ( всего 4 события)
А = { ОО; ОР} P(А ) = 2 : 4 = 0,5
B = { ОР; РР} P(В ) = 2 : 4 = 0,5
(+) А ![]() В = { ОР }
P(А
В = { ОР }
P(А ![]() В ) = 1 : 4 = 0,25
В ) = 1 : 4 = 0,25
P(А ![]() В) = P(А ) ∙ P( В )
В) = P(А ) ∙ P( В )
0,25 = 0,5∙ 0,5 верно, значит, являются
4. Из ящика, где хранятся 5 желтых и 7 красных карандашей, продавец, не глядя, вынимает один за другим 3 карандаша. Найдите вероятность того, что:
а) все карандаши окажутся желтыми;
Решение.
(+) Всего событий 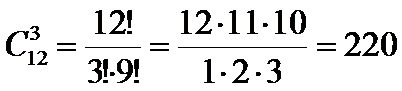
Благоприятных
событий 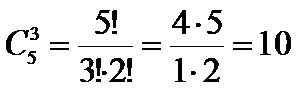
Вероятность 10 : 220 = 1/22
б) первые два карандаша — желтые, а третий — красный.
Решение.
(+) Всего событий 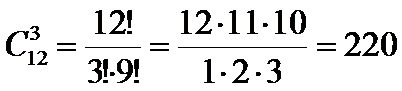
Благоприятных
событий 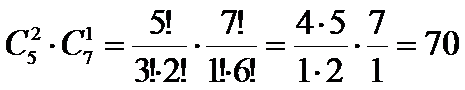
Вероятность 70 : 220 = 7/22
5. Случайным образом выбирается натуральное число от 1 до 50. Событие C — выбрано четное число. Являются ли события C и D независимыми, если событие D состоит в том, что:
а) выбранное число делится на 7;
Решение.
(+) Всего событий 50
Событие C — выбрано четное число.
N(C)= 25; P(C)= 25 : 50 = 0,5
Событие D - выбранное число делится на 7
N(D)= 7; P(D)= 7 : 50 = 0,14
Событие С![]() D - четное число,
делящееся на 7
D - четное число,
делящееся на 7
С![]() D = { 14; 28; 42
}
D = { 14; 28; 42
}
N(С![]() D)= 3; P(С
D)= 3; P(С![]() D)= 3 : 50 = 0,06
D)= 3 : 50 = 0,06
P(С ![]() D) ≠ P(C )
∙ P( D )
, значит, НЕ независимые
D) ≠ P(C )
∙ P( D )
, значит, НЕ независимые
б) выбранное число делится на 5.
Решение.
(+) Всего событий 50
Событие C — выбрано четное число.
N(C)= 25; P(C)= 25 : 50 = 0,5
Событие D - выбранное число делится на 5
N(D)= 10; P(D)= 10 : 50 = 0,2
Событие С![]() D - число делится
на 10
D - число делится
на 10
N(С![]() D)= 5;
P(С
D)= 5;
P(С![]() D)= 5 : 50 = 0,1
D)= 5 : 50 = 0,1
P(С ![]() D) = P(C )
∙ P( D )
, значит, независимые
D) = P(C )
∙ P( D )
, значит, независимые
Нормы оценок: «5» - 8(+); «4» - 6-7(+); «3» - 4-5(+)
Самостоятельная работа 4
по теме "Перестановки и факториал числа"
1. Домашнее задание по литературе состоит в том, чтобы выучить одно из трех стихотворений: "Анчар", "Буря" и "Вьюга". Миша, Никита и Олег решили распределить все три стихотворения между собой по одному. Сколько существует способов это сделать?
Решение.
(+) Количество способов соответствует количеству перестановок из трех элементов
3! = 6
2. Сколько различных последовательностей (не обязательно осмысленных) можно составить из букв слова "книга"?
Решение.
(+) Количество последовательностей соответствует количеству перестановок из пяти различных элементов
5! = 1∙ 2∙ 3∙ 4∙ 5 = 120
3. Вычислите значение выражения:
(+) а) 5! = 1∙ 2∙ 3∙ 4∙ 5 = 120
(+) б) ;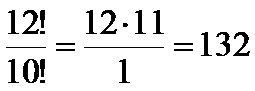
(+)
в) . 
4. Найдите вероятность того, что три последние цифры случайно выбранного телефонного номера — это цифры 2, 3, 1 в произвольном порядке.
Решение.
(+) Всего событий
(количество трехзначных чисел с возможным повторением цифр) 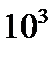
Благоприятных
событий (перестановки из трех цифр) ![]()
Вероятность 6 : 1000 = 0,006
Нормы оценок: «5» - 6(+); «4» - 5(+); «3» - 3-4(+)
Самостоятельная работа 5 по теме "Сочетания"
1. Вычислите: а) C72; б) C129.
2. В классе 20 учеников. Учитель решил проверить домашнюю работу у 6 из них. Сколько существует способов выбрать учеников для проверки?
3. Найдите вероятность того, что все буквы "а" окажутся на своих местах, если случайным образом перемешать и выстроить в ряд все буквы слова "карандаш".
4. На книжной полке 6 учебников и 3 сборника стихов. Найдите вероятность того, что среди случайно выбранных 5 книг окажется 3 учебника и 2 сборника.
Вариант 1
1. В барабане лотереи 20 одинаковых шаров. Шары пронумерованы от 1 до 20. Барабан вращается, и из него выпадает один шар. Найдите вероятность того, что номер шара — четное число.
2. В результате некоторого опыта с
вероятностью 0, 63 может наступить событие A, с вероятностью 0,
59 — событие B и с вероятностью 0, 22 — событие A ![]() B.
Найдите вероятность события A
B.
Найдите вероятность события A ![]() B. Является ли событие A
B. Является ли событие A
![]() B достоверным?
B достоверным?
3. Игральную кость бросают дважды. Найдите вероятность того, что в первый раз выпадет четное число, а во второй — число, большее чем 3.
4. В экзамене 6 вопросов. К каждому вопросу дано 2 варианта ответов, из которых только один вариант верный. Найдите вероятность того, что, отвечая наугад, ученик правильно ответит хотя бы на один вопрос.
5. В кармане у Буратино 5 золотых и 6 серебряных монет. Все монеты одинаковы по форме и размеру. Буратино, не глядя, вынимает из кармана 5 монет. Найдите вероятность того, что все эти монеты — золотые.
Вариант 2
1. Слово "Математика" написали на картонке и разрезали картонку на буквы. Буквы перемешали. Найдите вероятность вытащить наудачу картонку с гласной буквой.
2. В результате некоторого опыта с
вероятностью 0, 78 может наступить событие A, с вероятностью 0,
34 — событие B и с вероятностью 0, 11 — событие A ![]() B.
Найдите вероятность события A
B.
Найдите вероятность события A ![]() B? Верно ли, что событие A
B? Верно ли, что событие A
![]() B достоверное?
B достоверное?
3. Игральную кость бросают дважды. Найдите вероятность того, что в первый раз выпадет нечетное число, а во второй — число, меньшее чем 3.
4. В экзамене 5 вопросов. К каждому вопросу дано 2 варианта ответов, из которых только один вариант верный. Найдите вероятность того, что, отвечая наугад, ученик даст хотя бы один неверный ответ.
5. В вазочке на шкафу 4 конфеты с фруктовой начинкой и 5 — с молочной. Все конфеты одинаковы по форме и размеру. Маша дотянулась рукой до вазочки и, не глядя, выбирает 5 конфет. Найдите вероятность того, что все выбранные конфеты имеют молочную начинку.